Purpose

With GOTO computerized scopes being so prevalent, basic use of manual setting circles (also known as analogue setting circles) on a German equatorial mount (GEM) is not well covered in manufacturer instructions or basic astronomy books. This cheat sheet describes how to use manual setting circles. A reference table of bright stars with Bayer and Flamsteed numbers is provided here to aid in using manual setting circles. A table and spreadsheet of pre-computed slews for the Messier list and for the Caldwell list above -38° declination are provided. In aid of computerized GOTO small scopes, some of the tables include for bright reference stars, the identification cross-reference numbers to the HD and SAO catalogues. HD (Meade) and SAO (Celestron) handcontrollers typically contain one or both of these stellar catalogues. For GOTO resynching of a hand-controller, the table titled "Messier and Caldwell list slews from bright stars above -38° dec by Messier Caldwell number" is helpful. With this list, the telescope user can slew to the nearest bright star to the object, resynchronize their GOTO controller to that bright star and then slew the few remaining degrees to the faint object. Resynchronization of the hand-controller allows for high-accuracy slewing, in particular, for urban and suburban light polluted skies. Some astronomical planning software, like AstroPlanner, build in intermediate bright star slewing utilities that automate the resynchronization process. Basic concepts Manual setting circles best work by making short right-angle slews from bright-star targets. The telescope is centered on a bright star with known coordinates. The setting circles are adjusted to show the (1) known right ascension and declination of the target bright star, or to (2) zero (0 °) right ascension and zero (0 °) declination.

Declination and right ascension setting circles on a high-end mount - GNU Wikipedia Image by Halfblue

A short slew is then performed to move the scope either to (1) the direct right ascension and declination coordinates of the target or (2) the indirect index (offset index) between the bright star and the target. Special cases for indirect index slews involve where the bright reference star and object are on the same right ascension or declination great circle. These special cases are called (3) "right ascension sweep" and (4) "declination sweep".

As any of these techniques will rarely put the target exactly on center with visual observing alignment tolerances, this technique is supplemented with traditional star hopping. The use of bright stars with manual setting circles is similar to alignment stars in 1, 2 and 3 star computerized GOTO alignment.

A bright star chart

Some choices include: Tirion, W. and Skiff, B. Tirion Bright Star Atlas. Willman-Bell (accessed Sept. 2007). Tirion, W., Sinnott, R.W. 2000. Sky Atlas 2000. Sky Publishing (accessed Sept. 2007). Tirion, W. 2001. The Cambridge Star Atlas. Cambridge Press. (accessed Sept. 2007). Pasachoff, J.M., Tirion, W., Peterson, R.T.(ed). A Field Guide to Stars and Planets. Peterson Field Guides (accessed Sept. 2007) Uranometria 2000. Willman-Bell (accessed Sept. 2007).

Star Chart - Wikipedia GNU Image by T. Bronger

A bright star table with J2000 coordinates

Easy use of manual setting circles is dependent on having a good Bayer name list of bright stars above magnitude 4.5 that also lists the J2000 or epoch-to-date coordinates of each star. The list should be in hardcopy and sorted by constellation for ease of reference in the field. Bright star lists in several popular publications either do not have lists of sufficient star density or magnitude depth to allow for easy lookup. Tirion's Cambridge Star Atlas has a list of the 95 brightest stars, ordered by magnitude, down to about magnitude 2.5. Peterson's Star Guide and the RASC Observer's Guides have a comprehensive bright star list based on Garrison's catalogue of absolute magnitudes. Garrison's catalogue typcially contains 315 stars in both hemispheres down to a magnitude of 3.5. This is too low a density for use with setting circles (approx. 150 per hemisphere). These lists omits stars in some faint constellations, e.g. Capricorn, that only have faint stars.

A well-sorted comprehensive bright star list supplements the observer's preferred star chart which may identify the bright stars but not easy reference the J2000 coordinates for each bright star.

Some online bright star lists available on the internet that have both a good breadth and good order (Bayer and Flamsteed name within constellation) are:

• Richard Powells' Brightest Star List http://www.atlasoftheuniverse.com/stars.html accessed Sept. 2007. Lists 300 brightest stars to magnitude 3.5. Can be imported to Excel and resorted by right ascension and declination.
• UNSO Astronomical Almanac Bright Star List http://asa.usno.navy.mil/SecH/brightstars.html accessed Sept. 2007. Is available in pdf and ASCII tabular format for importing, sorting and filtering in Excel.
• UNSO Astronomical Almanac Bright Star Search Server http://asa.usno.navy.mil/SecH/bss.html accessed Sept. 2007. Will generate a list of bright stars, filtered by right ascension, declination and magnitude. That the list can be filtered by declination is useful for preparing charts for the latitude of your observing point.
• Harvard Bright Star Catalogue 5th Ed. http://vizier.u-strasbg.fr/viz-bin/VizieR?-source=V/50 accessed Sept. 2007. Can be used to generate filtered bright star lists by magnitude and declination in ASCII format for import into Excel.
• HD-DM-GC-HR-HIP-Bayer-Flamsteed Cross Index (Kostjuk, 2002) http://vizier.u-strasbg.fr/viz-bin/VizieR?-source=IV/27 accessed Sept. 2007. Can be used to generate filtered bright star lists by magnitude and declination in ASCII format for import into Excel.

Most of these lists can easily be imported into an Excel spreadsheet for easy sorting and filtering.

To aid northern North American observers near 41° North latitude, a filtered list of 638 bright stars down to magnitude 4.5, above -38° declination and sorted by constellation name and Bayer identification is provided here. The list is based on Kostjuk 2002. The list is limited to stars that have either a Bayer or Flamsteed identifier. (Html; pdf).

A low-power eyepiece with a precomputed true-field-of view

Once the scope is positioned using direct or indirect indexing, the target is acquired using the lowest feasible power eyepiece. Low power eyepieces yield the widest true-field-of-view (TFOV). A favored low-power eyepiece, typically 32mm, is used. Right ascension and declination can be measured by counting off the number of TFOV eyepiece views that the eyepiece traverses. To translate eyepiece views to right-ascension or declination, the TFOV of your favored eyepiece will need to be found by the following procedure:

• Lookup the apparent-field-of-view (AFOV) from your eyepiece manufacturer's website. Typically, the AFOV will be between 47° and 52°. If you cannot find a catalogue value, assume an AFOV 50°.
• The TFOV of the eyepiece is equal to the AFOV divided by magnification. TFOV=AFOV/M. Magnification is equal to the focal length of the telescope divided by the focal length of the eyepiece. TFOV=AFOV/(D_fl/EP_fl)=AFOV/M.

A worked example: I use a 32mm eyepiece with a 52° AFOV on a 1200mm fl telescope. The TFOV for that combination of eyepiece and telescope is:

1.4° = 52° / ( 1200 mm / 32 mm ) = 52° / 37.25x

With a field stop in the scope, the TFOV of this particular scope is closer to 1.2°. When pacing off eyepiece views, each view is overlapped to permit back-tracking across a star-field. The practical, working eyepiece TFOV of this telescope-eyepiece combination is about 1°. As a practical application, take M92, a globular cluster near iot Hercules. Using measuring calipers and a star chart, set the calipers equal to about one eyepiece TFOV, or 1° in the worked example. Use the declination degree scale on your chart to measure off one chart degree. Do not use the right ascension scale. Count off the number of eyepiece TFOV's in right ascension between iot Her and M92 - about 4° in right ascension and 3-4° in declination. Eyepiece views are overlapped to be able to backtrack the telescope. For the right-ascension leg of the iot Her to M92 slew, that translates with overlapping into 5 or 6 eyepiece views covering 4° decimal, as shown in the figure.

Counting e.p. TFOVs from iot Her to M92

Desireable resources

Drafting or divider calipers

Dividing calipers are used to step off the number of eyepiece views between the bright star and target, as shown on your star chart.

Dividing calipers - GNU Wikipedia Image by G. McKechnie

Extra watch set to local sidereal time

Before a night's observing, set a watch to local sideral time. This is the equal to your right ascension on the southern half of your meridian. The telescope is pointed at a star on the meridian and the right ascension manual setting circle can be adjusted accordingly. The USNO Local Sidereal Time Calculator can be used to set a secondary watch to local sidereal time on the observing night.

Watch - GNU Wikipedia Image by R. McLassus

Hand-magnifying glass

A hand-magnifier helps in read small text on charts by a dim red astronomy flashlight.

Hand-magnifer - GNU Wikipedia Image by Tomomarusan

In the first type - direct indexing - illustrated by the Orion EQ2 basic mount or the Orion Altas, the right-ascension setting circle moves with the scope and the right-ascension indicator remains fixed on the bottom half of the right-ascension portion of the mount.

In the second type - relative indexing - illustrated by the SkyView Pro EQ5, the right-ascension setting circle remains fixed. The right-ascension indicator moves above the fixed position setting circle on the bottom half of the right-ascension portion of the mount.

For both types of scopes, the indicator arrow on the right ascension tube and the declination tube can end up in hard-to-read positions.

A useful modification is to add indicator point lines at 120° intervals. To make a useful temporary mark, simply use copier white-out. If you are dissatisfied with the marks, rubbing alcohol will quickly remove them. Supplemental indicator markings can be made on both the right-ascension and declination barrels. Since all positions are made relative to any indicator line, having multiple indicator lines does not change the overall process of using a manual setting circle; it changes only the ease of reading the setting circle.

For the SkyView Pro EQ5 type mount, add three additional indicator marks on the right-ascension tube above the setting circle at 90° intervals. Add three additional indicator marks below the declination setting circle at 90° intervals.

For the Orion Altas EQ6 mount, make three additional indicator marks on the right ascension tube below the setting circle at 90° intervals. The Atlas EQ6 declination circle moves with the declination tube and the indicator is fixed on the right-ascension tube housing. Make the three additional marks on the fixed non-moving right-ascension tube below the declination circle. See the Supplemental Notes for a further discussion of marking the Orion Atlas (Syntax) EQ6 Goto mount.

For a basic mount like the Orion EQ2, after polaring aligning, point your scope at any star on the meridian. Then move your setting circle to the current local sidereal time.

Pre-compute the direct index coordinates or indirect index offset between the reference bright star and the target

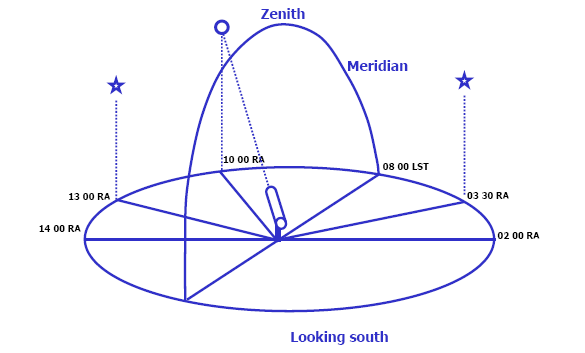
Three methods can be used to compute the size of the offset between a reference star and a target object - graphic, direct coordinates and indirect offset. Pre-computation and data lookup vary by the technique used:

• By the graphical method for indirect offset

  The example above for M92 illustrates using a chart and measuring calipers to determine the rough of amount of the index offset by counting the right-ascension and declination offset in terms of eyepiece views and decimal degrees.

• By direct index coordinates

  "Direct indexing" refers to setting the index circles to actual right-ascension and declination coordinates of the reference star and then the target object. To use the method, look-up the right-ascension and declination for both the bright reference star and the target object. E.g. for the M92 example above. Moving from iot Her to M92 involves a slight RA minus slew to the west and a minus declination slew to the south:

  Table: J2000 Coordinates of iot Her and M92

  Direction	Object	R.A.	Dec.
  To	M92	17h17m07"	+43°08m11"
  From	iot Her	17h39m28"	+46°00m23"
  Change		~-22m	~-3°

  After pointing at the bright star iot Her and slipping the right ascension and declination circles to reflect that star's coordinates, the corresponding change in the right ascension setting circle that results from you moving the telescope to the target is illustrated as follows:

  Slewing from iot Her to M92

  R.A. circle slipped to read RA 17h39m at iot Her

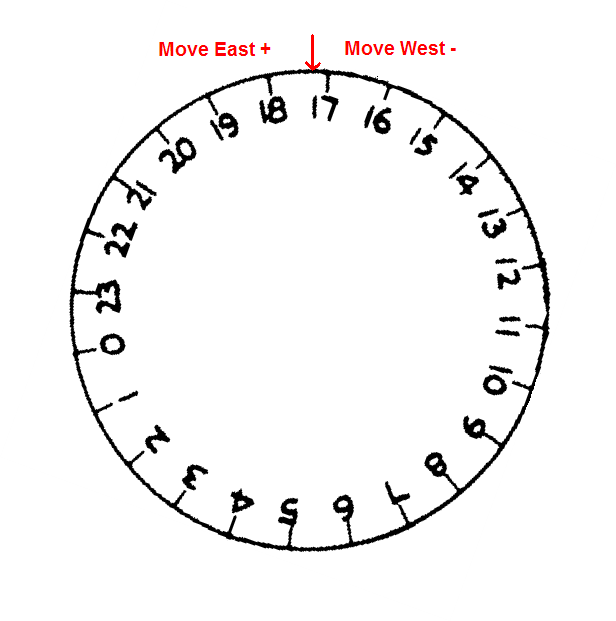
  R.A. circle after minus west slew to M92 at RA 17h39m

  The right angle slew only results in a small, subtle motion of the right ascension setting circle. The same process is applied to the declination tube of the mount and the declination setting circle's index.

  Whether you use the right ascension index mark on the tube placed by the manufacturer - or a supplemental white-out index mark that you added to your scope - does not change the result. The motion is relative to the bright star. As long as you reset (that is re-slip) the setting circle to the bright star's coordinates using an index mark of your choosing, that index mark will register the correct relative slew to the target.

  For deep-sky-objects like stars, clusters and galaxies, you can use catalogue J2000 coordinates - the object's position in the year 2000 - without determining their coordinates on the date of observation (the object's epoch-to-date coordinates). Deep sky objects move very slowly. Between a deep-sky-object and a bright reference star, their apparent relative positions will not change to a degree discernable visually for a over 100 years. In direct and indirect indexing, the scope is moved by the relative position between a bright reference star and the target.

  For solar system objects, like planets, find the epoch-to-date position of the planet because solar system objects are relatively fast moving with respect to any nearby bright star. Online resources to generate a ephemeris for a planet (a table of its right ascension and declination by date and time) include:

  • John Walker's "Your Sky" Online Planetarium program will display for your local horizon, a table that includes the epoch-to-date right ascension and declination for all the planets. In the Formilab online planetarium program, the universal time parameter can be set to your observing night and time.
  • NASA/JPL Online Horizon's Ephemeris Generator is more difficult to use than John Walker's planetarium program, but once mastered, it produces accurate detailed epoch-to-date ephemeris tables for any planet at down to minute level intervals. This is particularly useful for fast moving solar system objects like the Sun, comets, and the inner planets Venus and Mercury.

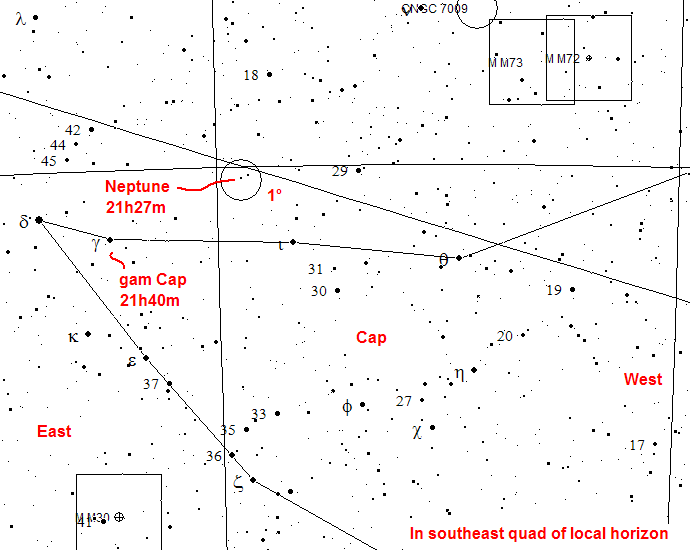
  As an example, on Oct. 7, 2007 at 3:00 UTC, the coordinates of Neptune (epoch-to-date) and of the nearest bright star, gam Cap in J2000, are:

  Table: J2000 coordinates of gam Cap and epoch-to-date coordinates of M92 for Salt Lake City, Utah

  Direction	Object	R.A.	Dec.
  To	Neptune	21h27m42"	-15°16m12"
  From	gam Cap	21h40m05"	-16°39m44"
  Change		~-13m	~+1°20m

  For Microsoft Office users, a simple slew calculator in Excel 2003 that computes these differences is provided.

• By subtraction for indirect index offset

  Indirect index offsetting is very similar to direct index slewing. The difference is you perform a little extra computation - the coordinates of the nearby bright reference star are subtracted from the coordinates of the target. See the example for Neptune and M92, above. If the RA difference is negative - the RA slew from the bright star to the target moves the telescope towards the western horizon. If the RA difference is positive, the slew from the bright star to the target moves the telescope towards the eastern horizon. In the preceding table, we have already found that moving from gam Cap to Neptune involves a slight minus RA slew (RA -13m) to the west and a plus declination slew to the north.

  After pointing at the bright star gam Cap, slip the right ascension and declination circles to read zero at any index mark of your choosing. The scope is then moved the relative index distance to the target. The corresponding motion of the right ascension circle that results from you moving the telescope to the target Neptune is illustrated as follows:

  Slewing from gam Cap to Neptune

  R.A. circle slipped to read RA0h0mm at bright reference star gam Cap

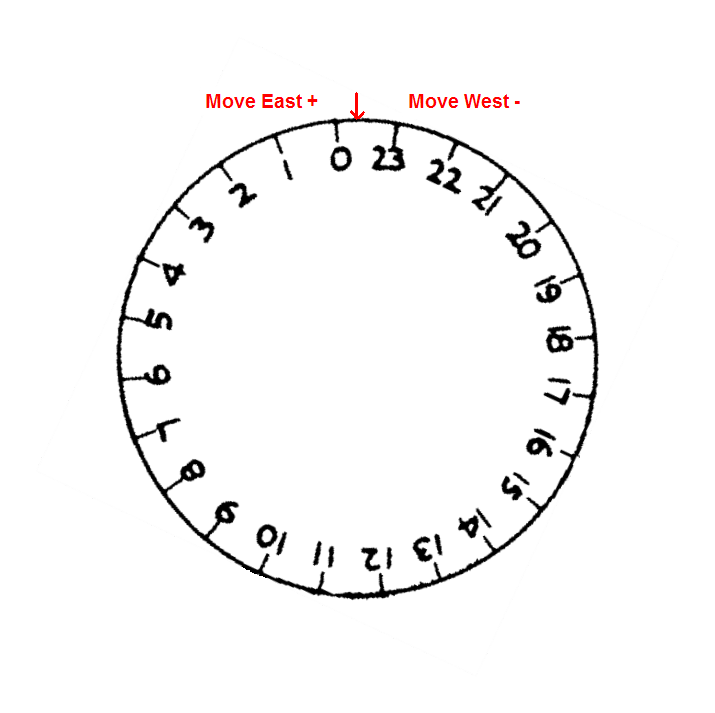
  R.A. circle after minus west slew to Neptune at offset index of RA -13m

  The process for the declination slew is the same, except it uses the declination setting circle.

Apply the direct or indirect index to the telescope

There are two methods to use manual setting circles: direct indexing or indirect offset indexing. A "RA sweep" or "Dec sweep" are a specialized case of an indirect index offset slew. A spiral search pattern is another search alternative.

For all methods, first lookup the coordinates of the nearby bright reference star and target and perform any needed pre-computation, as discussed above. Optionally, use a planetarium program to print a supplemental star hopping chart down to a deep magnitude, e.g - v10-13. Such a chart is useful to confirm faint planet and galaxy target acquistion and to aid in star hopping.

Direct indexing

• Unlock the scope and visually point and center in your eyepiece, the nearest bright star to your fainter target object. Relock the scope.
• Which right ascension setting circle index (the upper 0-24 or lower 24-0) that you use depends on the relationship of the scope's movement to the sky and the pointing of your scope in the eastern or western half of the sky. Just move the scope and see which right-ascension scale is matches the progression of right-ascension of the sky. For the northern hemisphere, usually the upper index marks matches the sky when facing south.
• Slip the right ascension and declination setting circles so they match the right ascension and declination coordinates of your bright star, read from the table above.
• Now unlock the scope or use the slow motion controls to right-angle slew the scope in declination and right ascension so the setting circles matches the coordinates of your target.

  You have two choices for slewing to the target - first slew in right-ascension followed by a declination slew or first slew in declination followed by a right-ascension slew (hence the term "right-angle slew"). The best choice for the first slew is the slew that ends at some bright star asterism.

  In the following left-hand illustration of slewing from bet CVn to M63, it is better to right ascension slew from bet CVn first, inorder to obtain the benefit of the asterism formed by 19 CVn, 20, CVn and 23 CVn. Then declination slew to M63. In the right-hand illustration of slewing from gam Cap to Neptune, first performing the declination slew is the better choice. This enables you to take advantage of the asterim formed by 42 Cap, 43 Cap and 44 Cap.

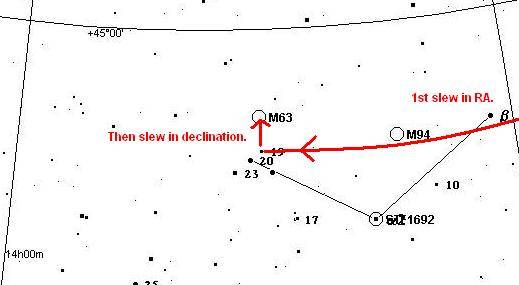
  Slewing from bet CVn to M63

  Slewing from gam Cap to Neptune

Indirect or offset indexing

• Pre-compute the index offset from the bright reference star to the target, using the reference table, as demonstrated above.
• Unlock the scope and visually point and center in your eyepiece, the nearest bright star to your fainter target object. Relock the scope.
• Which right ascension setting circle index (the upper 0-24 or lower 24-0) that you use depends on the relationship of the scope's movement to the sky.
• Slip the right ascension and declination setting circles so they both read RA0 and Dec 0 at your choosen index mark.
• Now unlock the scope or use the slow motion controls to right-angle slew the scope in declination and right ascension in amounts equal to the computed offsets.

Right ascension sweep and declination sweep

The example of finding M92 in Hercules illustrates the specialized right-angle slew cases of a right-ascension sweep and a declination sweep. M92 is located at nearly the same right ascension as a bright star between pi Her and rho Her - 69 Hercules. The difference in position between 69 Her and M92 is only in declination. A declination sweep is executed by centering on the bright reference star 69 Her. Then the telescope is swept in declination only until it pans across M92. At 69 Her, the declination setting circle is set to the star's declination coordinate: +37°17m30". The declination circle can be followed to approximate when M92 will pan into view.

Slewing from 69 Her to M92 or pi Her to M13

Nearby M13 and pi Her illustrate the converse case - a right ascension sweep. pi Her and M13 have nearly the same declination. The difference in their positions is only in right ascension. A right ascension sweep is executed by centering on the bright reference star pi Her. Then the telesocpe is swept in right ascension only until it pans across M92. At pi Her, the right ascension setting circle is set to the star's right ascension coordinate: RA17h15m. The right ascension circle can be followed to approcimate when M13 will pan into view.

Spiral search

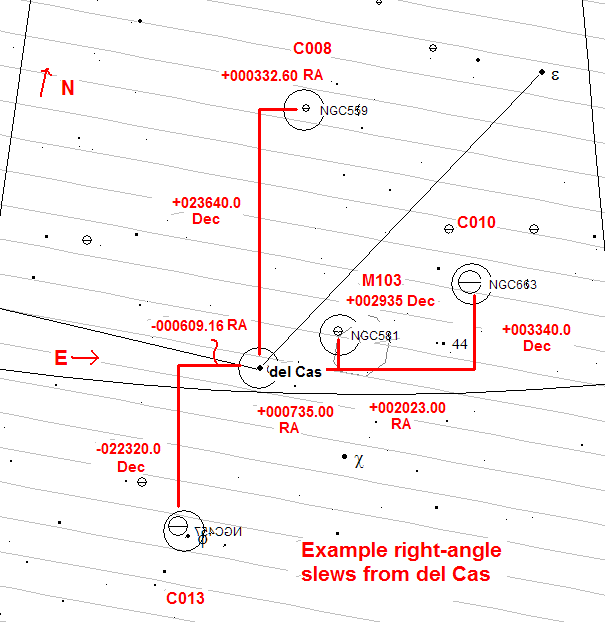
Sometimes a bright star or asterism is so close - within 2° of a target - that it is a simple matter to center on the reference object and the scan the adjacent eyepiece views for the target object. A spiral search pattern can be used to locate the target. Planetary nebula NGC6826 in Cygnus is illustrative. NGC6826 could be located by either a right-angle slew from iot2 Cyg, a right-ascension slew from theta Cyg or 26 Cyg, or by a declination slew from delta Cyg. Another method is to spiral scan after centering on bright star theta Cygnus. The search pattern, which links overlapping eyepiece views, is illustrated as follows:

Finding planetary nebula NGC6826

• Spreadsheet (Excel): Messier and Caldwell list for alt-az slews from bright stars above -38° dec by bright star (2.5 megs)

A user guide for the spreadsheet is provided below.

Converting a minute of right ascension to an arcminute of declination

A minute of right ascension (RA) is not equal to an arcminute of declination - that is an arcminute measured in decimal degrees. Right ascension can be converted to declination mathematically in order to find the number of decimal degrees and the equivalent eyepiece TFOVs in a right-angle slew.

When graphically measuring eyepiece views using a dividing caliper, the declination scale is used to measure one degree. Declination is measured in decimal degrees. Right ascension is a hybird measurement of time and angular distance in decimal degrees. The angular size of a minute of right ascension is not the same as angular size of an arcminute of declination. Furthermore, the angular size of a minute of right ascension shrinks as you travel from the celestial equator to the celestial north or south poles. This occurs because all the great circle lines of declination converge to points at the north and south poles. The practical implication is if you want to determine the number of TFOV eyepiece views to slew in right ascension by computation (a.k.a. reduction) there is some trigonometry to apply. Hence, it is easier, although less accurate, to use measuring calipers to measure the number of degrees involved in a right-ascension slew.

The varying angular size of right ascension in terms of decimal degrees

Mathematically, there are 15 minutes of right ascension for each arcminute of declination at the celestial equator. For example, take the slew to our worked example of finding Neptune - a right ascension slew distance of 13 minutes right ascension. Ignoring that Neptune is about 15° below the celestial equator, 15 times 13 RA minutes equals 195 declination (decimal degree TFOV) arcminutes. Dividing by 60 arcminutes per degree gives a right ascension slew of about 3 1/4° decimal degrees - or about 3 eyepiece views in the worked example. 3 1/4° is about the right ascension distance you would pace off using dividing calipers on a finder chart for Neptune. As you move further in declination away from the celestial equator, the more pronouced the shrinking size of a minute of right ascension becomes. Take our worked example of slewing the right-ascension leg between iot Her and M92 - a distance of 23 minutes of right ascension but at +47° declination.

Slewing from gam Cap to Neptune

Mathematically, the shrinking decimal degree angular size of right ascension is compensated by an additional multiplier of cos(declination) times 15 decimal arcminutes for one right ascension minute. (See Supplemental notes.) Rather than getting bogged down in trignometry, the following is a simple rough conversion table:

Table: Multiplier to convert right ascension to TFOV decimal degrees at various declinations Declination Cos(Declination) 15 arcmin decimal / 1 arcmin ra Multiplier 80 0.17 15 2.6 70 0.34 15 5.1 60 0.50 15 7.5 50 0.64 15 9.6 40 0.77 15 11.5 30 0.87 15 13.0 20 0.94 15 14.1 10 0.98 15 14.8 0 1.00 15 15.0

Slewing from iot Her to M92

In the M92 example, the right ascension slew of 22-23 arcmins of right ascension is equal to about 3.8-3.9° decimal ( [23 * ~10 multiplier ] / 60 arcmins per decimal degree). If you measure the declination degrees on a star chart and the right acension slew leg between iot Her and M92 (without any overlap as shown in the figure above), it is about 4 times the size of a declination degree mark on the chart.

In summary, to mathematically convert the right ascension slew in arcmins of right ascension to declination, estimate the multiplier from table provided above, or use the general formula:

arcmins decimal = 15 x arcmins right ascension x cos(radians(declination))

decimal degrees = arcmins decimal / 60

See M92 example, above.

Find Neptune

See Neptune example, above.

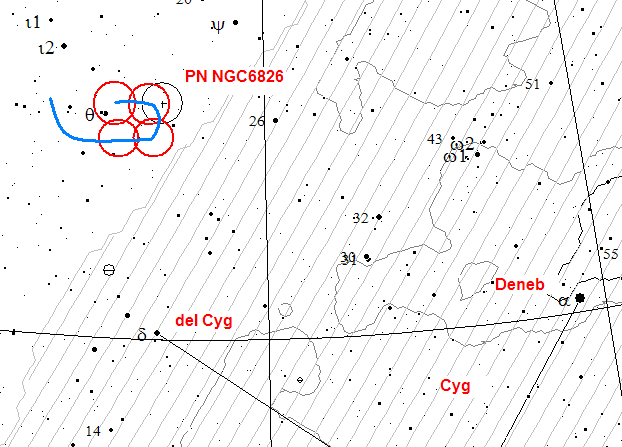
Find Planetary Nebula NGC6826

See NGC6826 example, above.

Garrison, R.F. & Beattie, B. 1996. The Brightest Stars. Url: http://www.astro.utoronto.ca/~garrison/oh.html accessed Sept. 2007.

Kostjuk N.D. 2002. HD-DM-GC-HR-HIP-Bayer-Flamsteed Cross Index. CDS Cat. IV27. Url: http://cdsarc.u-strasbg.fr/viz-bin/Cat?IV/27 accessed Sept. 2007.

MacRobert, A.M. 2007. The Setting Circles on Your Telescope. Sky & Telescope Online Article. Url: http://www.skyandtelescope.com/howto/visualobserving/3304206.html?c=y&page=1 accessed Oct. 2007.

Acknowledgements

Centre de Données astronomiques de Strasbourg - Catalogue Service: This project has made use of numerous catalogues redistributed through the CDS Astronomer's Catalogue Service, operated at CDS, Strasbourg, France. The use of those sources by this reference is acknowledged and appreciated.

Chevalley, Patrick: Cartes du Ciel Planetarium Software. This project makes use of celestial charts prepared using Cartes du Ciel v. 2.76. The use of this source by this reference is acknowledged and appreciated.

No copyright asserted

No copyright is asserted to any original content materials developed and included by this author in this document and the same are released to the public domain. No copyright is asserted as to any scientific fact recited herein or to any external content materials incorporated in this document.

Site tracking by:

Revisions

• 10-10-2007: Corrected "arcminute of right ascension" to "minute of right ascension.
• 03-09-2008: Merged and expanded with Messier and Caldwell list pre-computed slewing tables.
• 03-10-2008: Added Cartes du Ciel external catalogue file
• 03-14-2008: Added simple slew calculator
• 03-26-2010: Revised Messier Caldwell slew tables for SAO reference star numbers
• 10-31-2010: Added cross-reference table for 1822 stars brighter than mag 5.5 - Bayer-Flamsteed-to-SAO