How does the following table comport with your personal experience of atmospheric extinction?
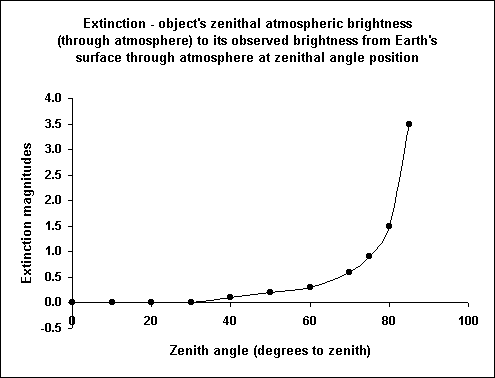
Table 3 - Extinction magnitudes Altitude z delta_m_z - zenith to object 90 0 0 80 10 0 70 20 0 60 30 0 50 40 0.1 40 50 0.2 30 60 0.3 20 70 0.6 15 75 0.9 10 80 1.5 5 85 3.5
The extinction equation (1.0) states a relationship between the brightness of a star outside the atmosphere.
Where:
Another value commonly used is m_z:
m_z = the magnitude of a star seen through 1 unit of air mass, typically, the zenithal limiting magnitude of a star seen through smallest air mass possible - that at the observer's zenith.
In astronomy, the baseline used for measuring extinction preferentially is the angle from the zenith to the object. The reason for this is that two observers can easily measure the same zenith angle. Your equatorial mounted scope is simply allowed to drop vertical and then is fixed with a vertical bubble level. Then using an index ring on the scope, the zenith angular distance is measured to the object.
The local horizon altitude of an object is a more nebulous concept, since no two observers have a clean line of sight to their horizon. For example, in my north Utah mountainous terrian, there are maybe one or two 5 degree sight lines that cleanly go to the horizon.
Where the zenith angular distance (zenith to object) is used, the air mass X between the observer and the stellar object approximately is:
X_obs = sec(z) = 1/cos(z) (2.0)
If you use the altitude "theta" (horizon to object), then:
X = sec(90-theta) = 1/cos(90-theta) (2.1)
When viewed at the zenith, the observer looks through the minimum possible air mass or sec(z 90 degrees) equals 1. Where the zenith limiting magnitude is determined from a star chart, which charts the apparent brightness of stars through the atmosphere at the zenith, the actual brightness would be somewhat higher, if the star were viewed outside the atmosphere, e.g. for a typical excellent ZLM sky of 6.5 mags:
m_oatm = 6.5 + k'*(sec(0 degrees)) , or
m_oatm = 6.5 + k'* (1)
If the extinction coefficient is 0.3, than the stars seen from space outside the atmosphere would be seen with the naked eye down to 6.8 mags.
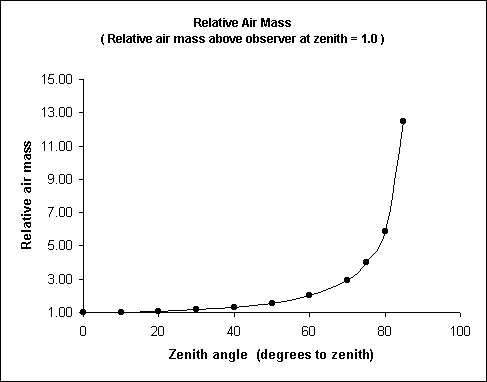
The air mass scalar X ranges from 1 at the zenith to about 12.5 at 5 degrees above the local horizon.
Table No. 1 Altitude z cos(z) sec(z)=Air mass 90 0 1.00 1.00 80 10 0.98 1.02 70 20 0.93 1.07 60 30 0.86 1.16 50 40 0.76 1.31 40 50 0.64 1.56 30 60 0.50 2.00 20 70 0.34 2.94 15 75 0.25 4.00 10 80 0.17 5.88 5 85 0.08 12.50
At the visual light bandwidth, k is _empirically_ known to be approximately linear, although it is effected by atmospheric water content - humidty - and by altitude of the observer. This is not true in the infrared. Schlosser 1991.
Bear in mind that m_z and m_obs are logarithmic stellar magnitudes - they are not expressed in units non-exponential brightness or incidence I. m_z is usually a fainter star but larger number than the brighter but smaller magnitude m_obs (e.g. a zenithal 7.5 is fainter than a lower but known to be brighter 5.5 star).
m_obs is the magnitude of the faintest star at a lower altitude from standard star charts or catalogues. It is not the photographically or photoelectrically measured brightness of a star as seen at the lower altitude. The m_obs, charted magnitude, is based on the brightness of the star, if it were at the zenith.
If k' is linear, how can it's slope be estimated?
Take two known pairs of x,y coordinates along the slope of k', the magnitudes (m_z and m_obs) and their estimated air masses (X_z and X_obs):
x_1, y_1 = m_z, X_z
x_2, y_2 = m_obs, X_obs
The slope of k' is negative and is approximately delta x / delta y, or:
k' = (m_obs-m_z) / (X_obs-X_z) (3.0)
The result of (3.0) would normally be negative. But stellar magnitude is a reverse scale - zenith stars are fainter but have larger numbers than and the observed lower fainter but brighter extinction stars.
But k' is positive in 1.0. Multiplying by negative 1 to correct for the reversed stellar magnitude scale gives the correct sign and therefore:
k' = (m_z-m_obs) / (X_obs-X_z) (3.1)
The object is lower in the sky than the zenith, so sec(obs) > sec(zenith) and X_obs-X_z is also positive.
Therefore, k' is positive.
If X_z is at the zenith, i.e. - the altitude of 90 degrees or z of 0, then:
k' = (m_z-m_obs) / (X_obs-1) (3.2)
This coefficient k' is a rate that states for 1 secant radians from the zenith, how many magnitudes of extinction occur? This coefficient is multiplied by a scalar, the observed object's number of secant radians from the zenith, the result is the total extinction in magnitudes. The secant radians from the zenith is also a scalar for the relative air mass between the observer and the object.
The starting point, the apparent brightness of star absent any atmosphere ( X = 0 ) can be linearily interpolated back from the slope of k' and the known ZLM.
Table 2 shows the results of a hypothetical k' of 0.3 and a ZLM sky of 6.5, interploated back to an outside atmosphere brightness of 6.8 mags:
Altitude z AirMass k' m_oatm m_obs delta_m_oatm delta_m_z 90 0 1.00 0.3 6.8 6.50 0.30 0.0 80 10 1.02 0.3 6.8 6.49 0.31 0.0 70 20 1.07 0.3 6.8 6.48 0.32 0.0 60 30 1.16 0.3 6.8 6.45 0.35 0.0 50 40 1.31 0.3 6.8 6.41 0.39 0.1 40 50 1.56 0.3 6.8 6.33 0.47 0.2 30 60 2.00 0.3 6.8 6.20 0.60 0.3 20 70 2.94 0.3 6.8 5.92 0.88 0.6 15 75 4.00 0.3 6.8 5.60 1.20 0.9 10 80 5.88 0.3 6.8 5.04 1.76 1.5 5 85 12.50 0.3 6.8 3.05 3.75 3.5

k', the extinction coefficient, is the slope of the linear relationship between air mass and magnitudes of extinction, shown in Equation (1.0).
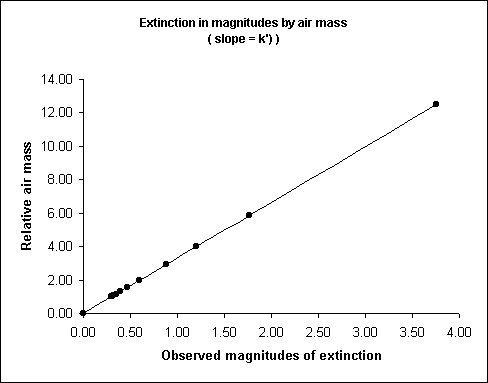
Table 2 is simplified in Table 3, which shows the extinction from ZLM, as observed through 1 relative air mass, in magnitudes by altitude of the object or its zenith angular distance:
Table 3 - Extinction magnitudes Altitude z delta_m_z - zenith to object 90 0 0 80 10 0 70 20 0 60 30 0 50 40 0.1 40 50 0.2 30 60 0.3 20 70 0.6 15 75 0.9 10 80 1.5 5 85 3.5

Table 2 nicely approximates the extinction magnitude by zenith angular distance in Sidgwick's Figure 178 at 449. Sidgwick 1971.
A supplemental worksheet in Excel 2000 format is provided modeling the above equations. The Excel file contains some of my personal macros. If you are concerned about macro viruses, use the "Disable macros" options, when Excel loads the file.
Substituting equation 3.2 into 1.0, the expansion is:
m_oatm = m_obs + ((m_z - m_obs) / (X_obs-1)) * (sec(z)) (4.0)
The reference object does not have to be at the zenith. It might also be off zenith, in which case, equation 3.1 applies and the expansion is:
m_oatm = m_obs + ((m_z-m_obs) / (X_obs-X_z)) * (sec(z)) (4.1).
This gives only a crude approximate estimate of extinction and does not account for effect of humidity or the effect of altitude above mean sea level.
The measurements usually are made by estimating the naked-eye unmagnified, limiting magnitude (NELM) at the zenith (ZLM) using standard star charts or catalogues. The zenithal faintest bright star is m_z in equation 3.1. A second star is used between 5 to 10 degrees above the local horizon to establish a horizonal NELM. The horizonal NELM is estimated by noting the degrees of the horizon that a known bright stars first become visible. At my forty-one degree north location during the winter months, such horizonal stars might be alpha Columbia (v2.3), pi Puppis (v2.7) or zeta Puppis (v2.7) on the southern horizon, the stars in the tail of Leo as it rises in the east, or stars in the circlet of Pisces as it sets in the west.
Another possible option for taking these measurements is to use the telescopic or binocular limiting magnitude of open cluster NGC1647 as moving reference beam of known intensity.
The higher zenithal object does not have to be "at the zenith" to apply, so:
k' = (m_z-m_obs) / (X_obs-X_z) (3.1)
It only has to be significantly higher than the m_obs object so an extinction effect occurs, whether caused by atmospheric particles, humidity or light pollution.
NGC1647 might be used as moving reference beam. Measure m_z when NGC1647 is high in the sky. That provides m_z. Wait a couple of hours until NGC1647 is at a lower altitude in the local western sky and measure again. That is m_obs.
For light pollution, a scope's limiting magnitude can be calibrated using my NGC1647 charts when NGC1647 is near the local zenith in an excellent rural sky, using a small telescope or binocular and a set low magnification. Repeat the measurement in a light polluted urban area. The difference in magnitudes can be used to make a crude numerical estimate of the change in the coefficient k' that shows the effect of light pollution, in addition to the raw magnitude difference at the zenith. My personal experience with NGC1647 in light polluted skies using low magnification and a low aperature is that is gives a good limiting magnitude response between v8.0 and v10.5, but I have explored this systematically.
This is an amateur observer effort. All criticisms and correction of any errors is solicited and welcomed.
Please provide any comments via email to:
Kurt Fisher fisherka@csolutions.net Last updated: 3/4/2004
Sidgwick, J.B. 1971. Amateur Astronomer's Handbook. 3rd ed. Dover. Section 26.2 at pp. 446-445
Duffet-Smith, P. 1988. Practical Astronomy with your calculator. 3rd ed. Cambridge Press. Section 43 at p. 83
Minnaert, M. 1954. The Nature of Light and Colour in the Open Air. Dover.
Schlosser, W., Schmidt-Kaler, T., Milone, E.F. 1991. Challenges of Astronomy. Springer-Verlag. Section 19.5 at pp. 100-103