Which way is the Earth moving? - An amateur astronomy primer
Summary
This note discusses how to determine at key times - like sunset, sunrise, solar noon, and solar midnight, and the First Quarter, Full and Third Quarter Moons - the direction that the Earth is revolving around the Sun with respect to an observer's local horizon. This is in aid of appreciating the Earth as an object that is moving through three-dimensional space.
This note provides an overview and illustrations explaining these concepts for use at astronomy club star parties.
This note uses many illustrations of orbits of the Earth and Moon generated using the NASA/JPL Solar System Live online planectia. NASA and JPL graciously allow free redistribution of Solar System Live images for non-commercial purposes.
All example illustrations are based on an observing point in the Intermountain western United States at about latitude 41° North.
Discussion
Visualizing the Earth's orbital path with daily life analogies
|
The Earth can be visualized as a bus driving down a highway with a set of street lamps or telephone polls standing on either side of the road or a person walking down a path with a row of trees planted on either side. In a car on highway or when walking down a path, movement forward creates the visual illusion that the street lights, telephone poles or trees increase in apparent size as we move toward them and then reduce in apparent size as they recede the distance behind us. The constellations also appear to move towards us and then recede behind us as the Earth travels through space. One difference is that since the Earth orbits in a nearly circular path, that the same set of "trees" or constellations - appears again and again in a repeating cycle.
|

Figure 1 - Apparent motion of street lamps lining
both sides of an urban street.
Public domain image by author.
|
In the case of the Earth, there are two movements - the Earth is revolving around the Sun over the course of one year - in a counter-clockwise fashion when looked at from above the North Pole - and Earth rotates on its axis over the course of one day - also in a counter-clockwise fashion.
A daily life analogy would ice or roller skating around a rink. Skating around the perimeter of the rink simulates the Earth revolving around the Sun; while an ice-skater twirling in-place simulates the rotation of the Earth about its axis. Children can easily simulate this by walking around the perimeter of a large room in a counterclockwise direction, while simultaneously rotating around their central axis. Under these conditions, your view of the surrounding room becomes confused. Reading signs posted on the side of room becomes difficult.
|

Figure 2 - Skaters moving counterclockwise around
the perimeter of a public ice rink in Salt Lake City.
Image by author, public domain.
|
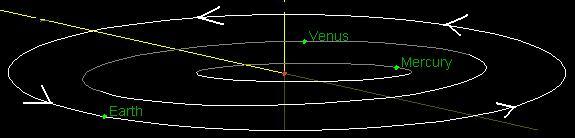
Figure 3 - Earth revolving around the Sun
in a counterclockwise direction.
Image courtesy NASA/JPL-Caltech
|
|
|

Figure 4 - Ice skater spinning in place.
Public domain image from Wikimedia-commons
|

Figure 5 - Earth rotating counterclockwise.
Public domain animation. View
Galileo Time-Lapse Photography of Earth's Rotation
|
To simply our confusing view of the night sky, night time observers typically cancel the effect of the Earth's rotation by looking at the sky once a night at the same time - typically around 9:00 pm or midnight local time. With this nightly snapshot view, the effect of the Earth's rotation is cancelled and we see the night sky changed only by the Earth's revolution around the Sun. Compared to our experience driving in a car, the night sky moves toward us at a snail's pace. When looking due south between two successive nights at the same time, a star appears to move only about 0.9° - or about the width of your index fingertip at the end of an outstretched arm.
|
Our daily life analogy to the Earth revolving around the Sun also can be simulated by riding the driver's side of a car (American left-hand driver's design) going counter-clockwise around a city block. The Sun is the middle of the city block out the driver's window to the left. The outside of the block has stores, office and residential buildings.
The outside view through the passenger's window - to the right of the driver - is analogous to the zodiacal constellations on the night sky's celestial dome. The passenger in a terresterial car see a repeating procession of the same businesses, parking lots and storefronts each time the driver and car "orbits" the building at the center of the block. As the Earth revolves around the Sun, a repeating procession of constellations are viewed to the "outside" of the Earth's orbital path over the course of one year at 9:00pm and over the course of each 24 hour period as the Earth rotates on its axis.
|

Figure 6 - Driving around a city block in a counterclockwise direction.
|
Figure 7 - Constellations of the ecliptic. Image from NASA
|
In this sense, as you face due South on successive mornings at the same hour before sunrise
, you are riding on the planetary bus - the Earth. The constellations move toward you on successive mornings and recede over the western horizon in the same way that streetside objects appear to move towards you and then recede in the distance.
Key orbital geometries to find the direction that the Earth moves along its orbital path
|
At sunset and sunrise, the Sun is tangent to the surface of the Earth where an observer's stands.
|
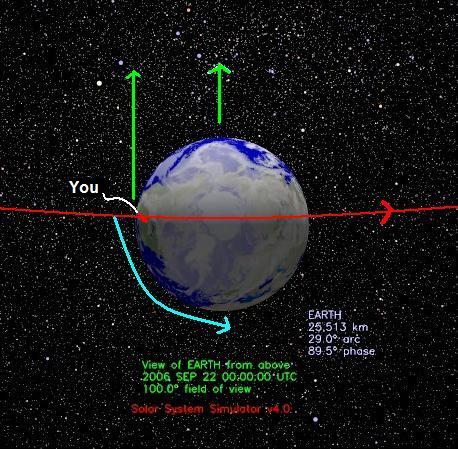
Figure 8 - View of Earth from above
at sunset in the western U.S. on 9/21/2006. Image courtesy NASA/JPL-Caltech
|
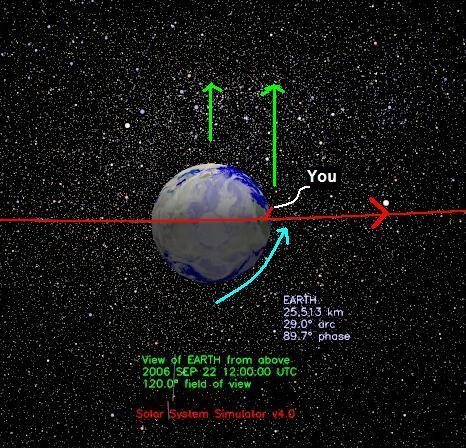
Figure 9 - View of Earth from above
at sunrise in the western U.S. on 9/22/2006. Image courtesy NASA/JPL-Caltech
|
Knowing that:
- the Earth revolves in a rough circle around the Sun during the across of a year in a counterclockwise direction,
- the Earth rotates on its axis once a day also in a counterclockwise direction; and,
- a sunset and sunrise, the Sun is tangent to the surface of the Earth where an observer's stands,
- we can make some deductions about which way the Earth is moving at sunset and sunrise.
At sunrise, when we face due south, the East is on our left (in the northern hemisphere) and the West is on our right-hand. The sun is rising in the East and is just tangent to the surface of the Earth where you are standing.
|

Figure 10 - View of local horizon in western U.S. on 9/22/2006 at sunrise.
Image from Cartes du Ciel
|

Figure 11 - View of Earth from above at sunrise
in the western United States on 9/22/2006.
Image courtesy NASA/JPL-Caltech
|
The implication is that the Earth in its revolution around the Sun is moving on a path that goes through the center of the Earth and in a direction almost directly over your head - the observer's zenith.
At sunset, when we face due south, the East is on our left (in the northern hemisphere) and the West is on our right-hand. The sun is setting in the West and is just tangent to the surface of the Earth where you are standing.
|
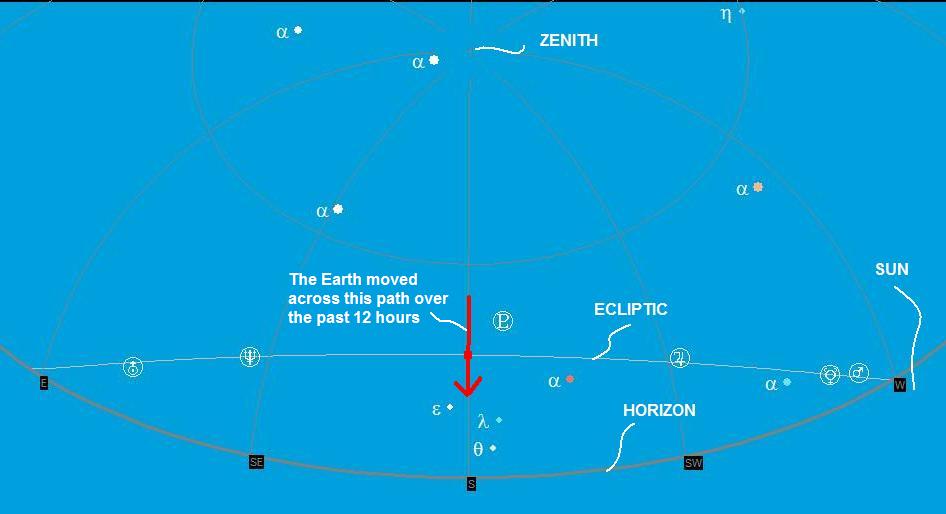
Figure 12 - View of local horizon in western U.S.
at sunset on 9/22/2006. Image from Cartes du Ciel
|

Figure 13 - View of Earth from above at sunset
in the western United States on 9/22/2006.
Image courtesy NASA/JPL-Caltech
|
The implication is that the Earth in its revolution around the Sun is moving on a path in a direction away from a direction almost directly over your head, albeit lower to the horizon - below the observer's zenith - and down through your feet and the center of the Earth. Looking up and due south, you are viewing "back" down the Earth's orbital path that the Earth traversed earlier that day.
Background knowledge and basic skills
Earth's orbital speed
The distance that the Earth has traveled is about 24 hours at 29.7848 kilometers per second (or 107,229.24 km/hour). That simplifies to:
- 24 hours * 29.7848 km/sec
- 24 hours/day * 60 minutes/hour * 60 seconds/minute * 29.7848 km/sec
- 24 * 60 * 60 * 29.7848 km/day
- 2,573,400 km/day
The semi-major radius of the Earth's orbit is 149,597,887.5 km. Applying the basic equation for a circle of 2*pi*r yields the approximate circumference of the Earth's orbital path of 939,951,248.7 km. (2 * 3.14159 * 149,597.887.5 = 939,951,248.7 km). Dividing by a mean orbital speed of 2,573,400 km per day yields 365.25 days - or about the length of the solar year.
Finding the time of sunrise, sunset, local solar noon and solar midnight
You will need to be able to find the time of sunrise and sunset. The time of sunrise and sunset is printed in the newspaper or the U.S. Naval Observatory Sunrise and Sunset for One Day Web applet will generate the information for you. You can also use the U.S.N.O. Astronomical Applications website to find the Universal Time Coordinated (UTC) for your location and the current hour offset to convert UTC time to your local time.
Major orienting points on the dome of your local horizon night sky
You will need to know some major orientation features in your local horizon coordinate system - of the dome of night sky as seen at night from a point on the Earth. Those key orientation features are:
- Due south
- Due east
- Due west
- Zenith - a point directly over your head
- Meridian - a great circle that passes through due south, your zenith and the North Pole near the star Polaris.
- Meridian south - the portion of your local meridian that passes through the zenith and due south.
- "To south", "souths", or "transit" - occurs when an object on the dome of the night sky with an altitude between your zenith and the due south passes - or "transits" your meridian south.
|

Figure 14 - Key points to orient the dome of the night sky. Image by Cartes du Ciel
|
Locating the ecliptic
You will need to be able to find the ecliptic on the night sky dome of your local horizon. The ecliptic can be traced on the dome of the night sky by gaining familiarity with the constellations of the zodiac, a band of constellations approximately 10°s above and below the ecliptic.
|

Figure 15 - Constellations of the ecliptic. Image from NASA
|
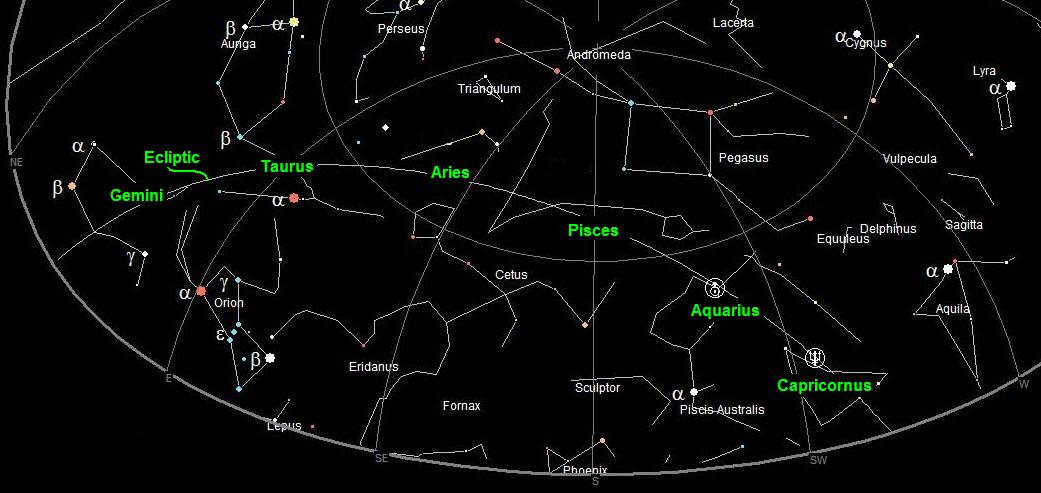
Figure 16 - Tracing the ecliptic
above local horizon using zodiac constellations. Image by Cartes du Ciel
|
Table 1. Constellations of the ecliptic (zodiac) for Longitude W111
| Name | Mnemonic | Month Sun is in | "Souths" at night during month near midnight | "Souths" at night during month at 9PM |
|---|
| Aries | A | May | Oct. | Dec. |
| Taurus | Tense | June | Nov. | Jan. |
| Gemini | Gray | July | Dec. | Feb. |
| Cancer | Cat | July | Jan. | March |
| Leo | Lay | Aug. | Feb. | April |
| Virgo | Very | Sep.-Oct. | Mar.-Apr. | May |
| Libra | Low, | Nov. | Apr.-May | June |
| Scorpius | Sneaking, | Dec. | May | July |
| Sagittarius | Slowly, | Jan. | June | August |
| Capricornus | Contemplating | Feb. | July | Sept. |
| Aquarius | A | March | Aug. | Oct. |
| Pisces | Pounce | Mar.-Apr. | Sept. | Nov. |
|
To be able to trace the ecliptic using the zodiac constellations requires some practice with a basic star chart or planisphere. Take a few moments to look due south around 9:00pm local time every four or five days and identify the progression of the constellations for one year.
|
The ecliptic also can be found using an online planetarium program like the Formilab's Your Sky Online Planetarium or Christian Legrand's or Patrick Chevalley's Cartes du Ciel freeware.
If using a planetarium program feels like a modern "cheat", it's not. The ancient Greeks used a similar technique with an analogue computing device called an armillary sphere. The noon shadow of the Sun was used to position the sphere so the Sun was aligned with the constellation that it was currently in. The sphere was then rotated as the Sun set, and the constellation at the intersection of the south meridian and the ecliptic at the moment of sunset could be read on the sphere's dial. The stars of the constellation could not be seen at sunset, but could be seen about an hour after sunset to the west of south.
|
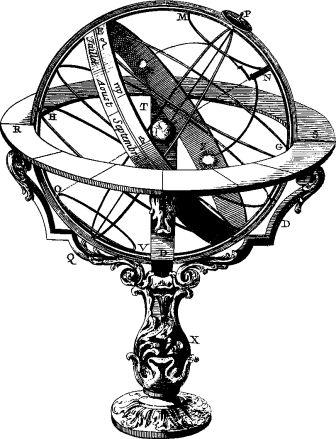
Figure 17 - An armillary sphere - public domain image from Wikipedia
|
Understand the tilt of the Earth's rotation and the tilt of the Moon's orbit around the Earth
The direction of Earth's travel is not exactly directly overhead at your local zenith at sunset or sunrise. The axis of the Earth is tilted at a 23 1/2° angle to the plane of the Earth and Sun - called the ecliptic. This tilt produces the seasons.
The Moon orbits the Earth and its orbit is tilted at about 6 degrees to the ecliptic. This means through a lunar month, the Moon moves between about 6 degrees above to 6 degrees below the ecliptic. If you hold a fist outstretched, six degrees is about two-thirds the distance across the top of your knuckles.
|
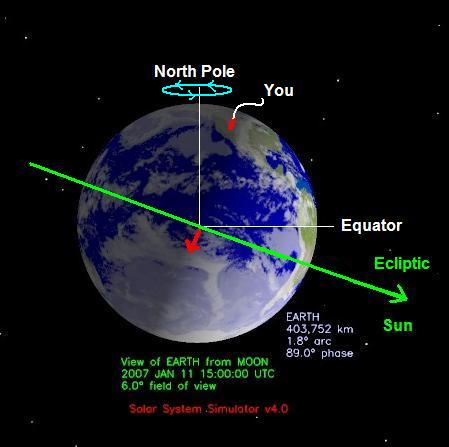
Figure 18 - Tilt of the Earth - view of Earth
from Moon on 1/11/2007
sunrise in western U.S.
Image courtesy NASA/JPL-Caltech
|

Figure 19 - Tilt of Moon's orbit with respect
to Earth's equator and ecliptic
|
The apparent size of the constellations on the horizon and at the zenith
The analogue to the motion of the constellations across successive nights to the linear motion down a highway is true with respect to the motion of objects. The analogy breaks down with respect to the size of approaching constellations on the dome of the night sky.
For terresterial movement on the Earth, perspective makes distant objects appear smaller. They appear larger as you drive closer to them. This holds true for solar system objects like the planets Mercury, Venus and Mars and the Moon. The closer the object, the larger its apparent angular size.
But constellations are at a relative infinite distance from the Earth. They are so far away with respect to the size of the orbit of the Earth that they do not change angular size if viewed in December as opposed to when viewed from the opposite side of the Earth's orbit during the following June.
The apparent size of constellations above your local horizon when viewed with the naked-eye is further confounded by an illusion generated by the human brain. Constellations near the horizon appear larger than usual and grossly distorted. They appear to grow smaller as they come "closer" near the zenith. The most common experience of this visual illusion is the "full Moon effect" where the Moon appears much larger when it rises over horizon as compared to when it nears the zenith. The effect is a visual illusion generated by the mind - when photographed with a camera at the horizon and at the zenith, the Moon does not change significantly in size.
There is a slight change in the apparent angular size of the Moon at the horizon due to the refracting effect of the Earth's thick atmosphere. This refraction is less at the zenith because there is less air directly over your head than when looking close to the horizon. This slight change in the apparent size of the Moon or Sun generally is only noticeable to the naked-eye when, for example, the Sun while setting is just about to touch the western horizon. At such times with Moon or Sun may appear slightly flattened instead of circular.
Because of this visual illusion and when viewing constellations with the naked-eye, their apparent size on the celestial dome is just the opposite of terresterial perspective.
On the Earth, a distant telephone appears smaller and grows larger as it approaches. On the night sky's dome, when a constellation first rises over the eastern horizon, the visual illusion makes it look larger. As it "approaches" our meridian and the zenith, the constellation appears to grow smaller in angular size relative to the its appearance at the horizon.
Finding the approximate direction that the Earth is moving around the Sun at key times
At sunset or sunrise
At sunset, when you look towards the path that the Earth is moving away from (or the 2,573,400 kilometers that it traveled across earlier in the day) that place on the ecliptic is invisible in the twilight. It can easily be located using online or local disk planetarium software, discussed above. After looking at your best guess for the direction of sunset and zenith at sunset, walk indoors and lookup where the ecliptic crosses due south on the horizon. Note down the constellation and nearest bright star.
Wait for the Sun to fully set and the constellations become visible. Then go back outside and look for the constellation and nearby bright star. This is the direction that you and the Earth are moving away from. The process is reversed for sunrise.
|
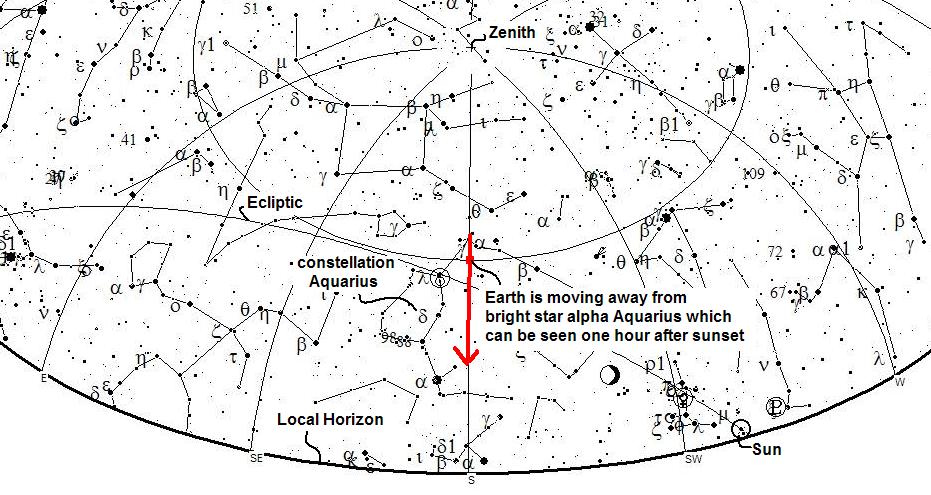
Figure 20 - Local horizon at sunset on 9/22/2006
in black and white using the planetarium program
Cartes du Ciel
|

Figure 21 - View of Earth from above
at sunset in the western U.S. on 9/22/2006.
Image courtesy NASA/JPL-Caltech
|
|
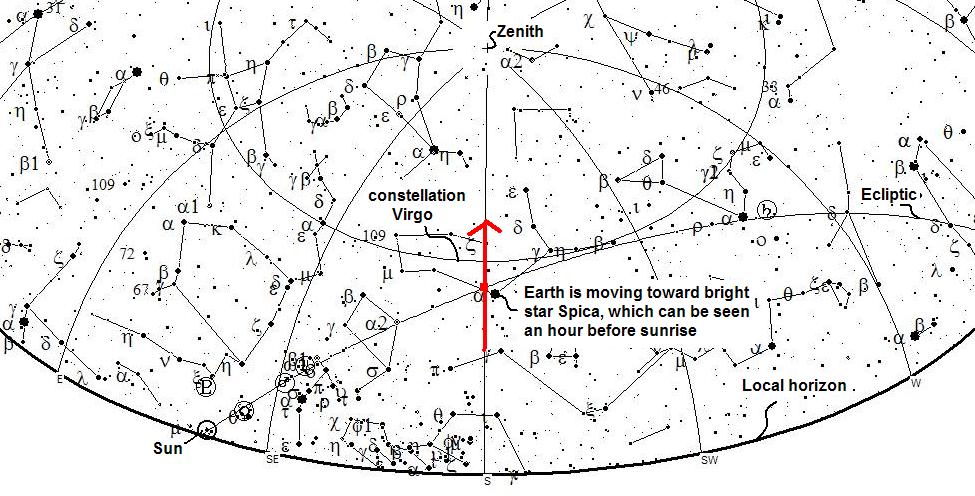
Figure 22 - Local horizon at sunrise on 9/22/2006
in black and white using the planetarium program
Cartes du Ciel
|

Figure 23 - View of Earth from above
at sunrise in the western U.S. on 9/22/2006.
Image courtesy NASA/JPL-Caltech
|
On the evening of the First Quarter Moon
The Sun, which sits in the ecliptic plane, and the Moon, which is usually near the ecliptic plane, can act as convenient markers of the ecliptic. You can use these markers to indicate the direction that the Earth is moving in its orbital plane at noon during the daytime, on the night of the full Moon, and on the night of first quarter and third quarter Moon.
For the first quarter Moon at sunset, the Moon is 90° from the Sun and 180° behind the path down which the Earth is revolving around the Sun. In the sunset twilight, the first-quarter Moon is visible in the evening sky. The Moon sits close to the ecliptic. When you are looking at the Moon, you are looking "down" the approximate path that the Earth has traveled across that day.
|
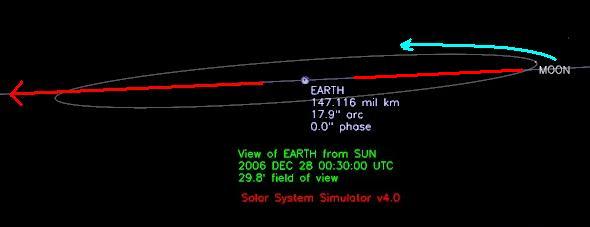
Figure 24 - Orbital path of the Moon relative to the Earth at First Quarter Moon on 12/28/2006 at 00:31 UTC as seen from the Sun. Image courtesy NASA/JPL-Caltech
|

Figure 25 - Local horizon at First Quarter Moon on 12/27/2006 near sunset. Image from Cartes du Ciel
|

Figure 26 - View of Earth from above at sunset in the western United States on 9/22/2006. Image courtesy NASA/JPL-Caltech
|
On the evening of the Third Quarter Moon
For the third quarter Moon at sunrise, the Moon is 90° away from the Sun but sits in front of the path that the Earth is revolving around the Sun. The Moon is also near the ecliptic. In the morning twilight, the third quarter Moon is visible in the morning sky. When you are looking at the third-quarter Moon, you are looking "up" the path that the Earth will traverse across during the rest of the day.
|
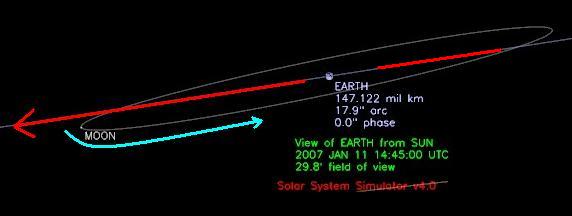
Figure 27 - Orbital path of the Moon relative to the Earth at Third Quarter Moon on 1/11/2007 at 14:45 UTC as seen from the Sun. Image courtesy NASA/JPL-Caltech
|
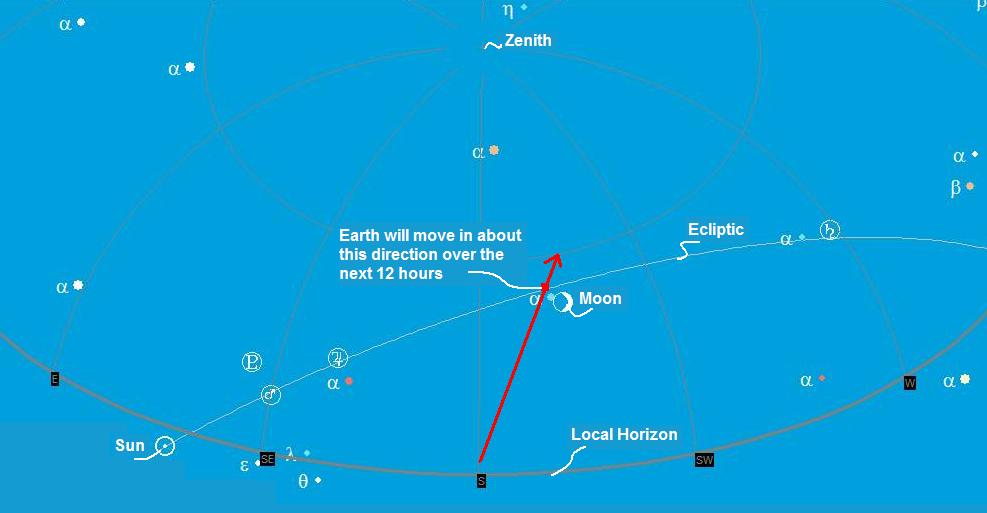
Figure 28 - Local horizon at Third Quarter Moon near sunrise on 1/11/2007 near sunrise. Image from Cartes du Ciel
|

Figure 29 - View of Earth from above at sunrise in the western United States on 9/22/2006. Image courtesy NASA/JPL-Caltech
|
On the evening of the Full Moon
The Full Moon can also be used to mark the direction of the Earth's travel. As the full Moon "souths" or crosses your local southern meridian, the Earth is moving towards your local due east and away from your local due west.
|

Figure 30 - Earth and Moon at Full Moon viewed from Sun on 1/3/2007 at 7:20 UTC. Image courtesy NASA/JPL-Caltech
|

Figure 31 - Earth and Sun at Full Moon viewed from Moon on 1/3/2007 at 7:20 UTC. Image courtesy NASA/JPL-Caltech
|
|
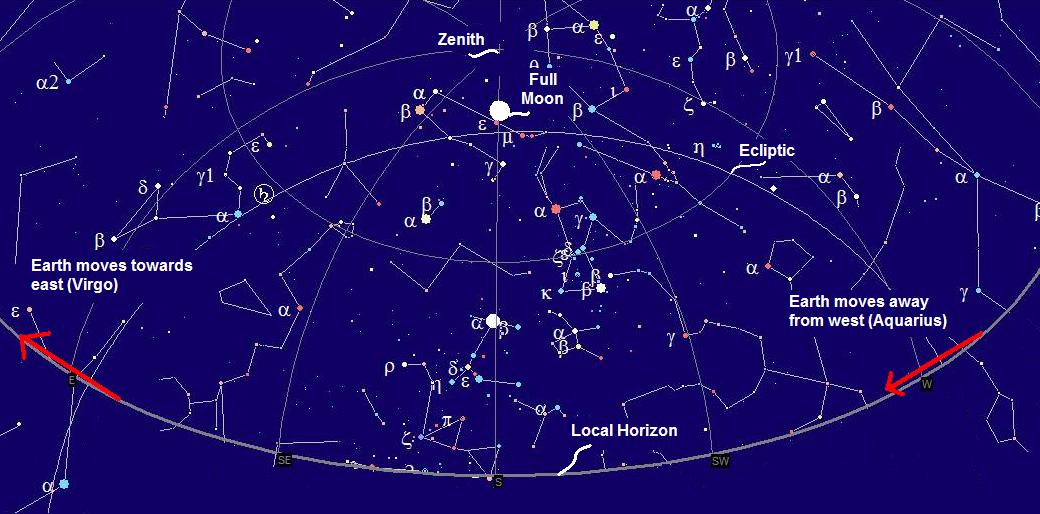
Figure 32 - Local horizon view looking south at Full Moon 1/3/2007 at 00:20 MST or 7:20 UTC. Image by Cartes du Ciel
|
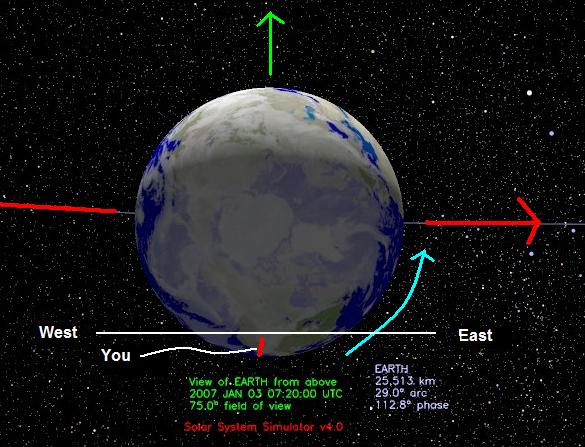
Figure 33 - Earth viewed from above at Full Moon on 1/3/2007 at 07:20 UTC. Image courtesy NASA/JPL-Caltech
|
At local apparent solar noon using the Sun and compass points
Although the stars are not visible in the daytime, you also can tell the direction that the Earth is moving using the noon Sun - another mid-point between sunrise and sunset. At local solar noon, the Earth is moving towards your due west and away from your local due east. To find the time of local solar noon, lookup of the time of sunrise and sunset that is printed in the newspaper or the U.S. Naval Observatory Sunrise and Sunset for One Day Web applet will generate the information for you. Apparent solar noon, the time that the Sun "souths" or passes your local south meridian is the mid-point between these two times - during the daytime. Apparent solar midnight, the time that the point opposite the Sun "souths" or passes your local south meridian is the mid-point between these two times - during the night-time.
|
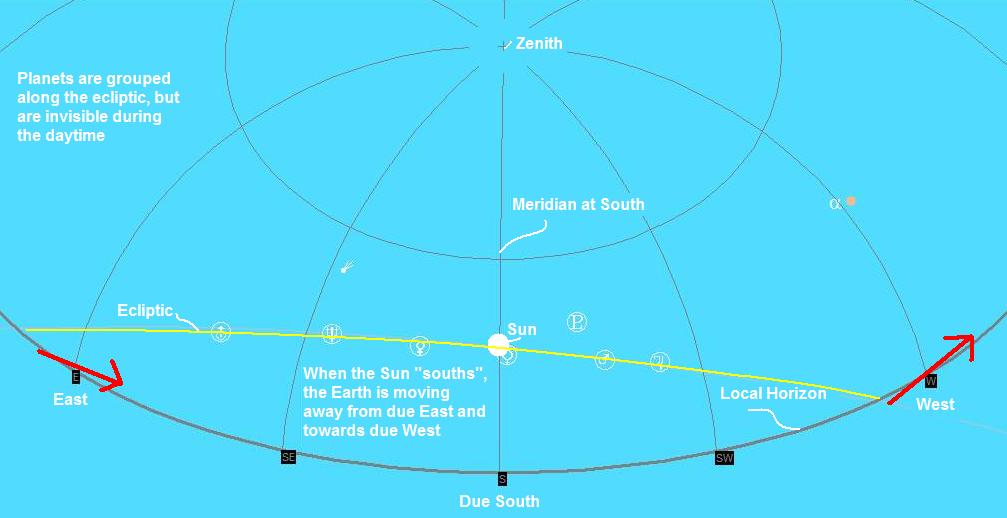
Figure 34 - Local horizon at solar noon on 1/3/2007 at 12:31PM local time. Image generated by Cartes du Ciel
|
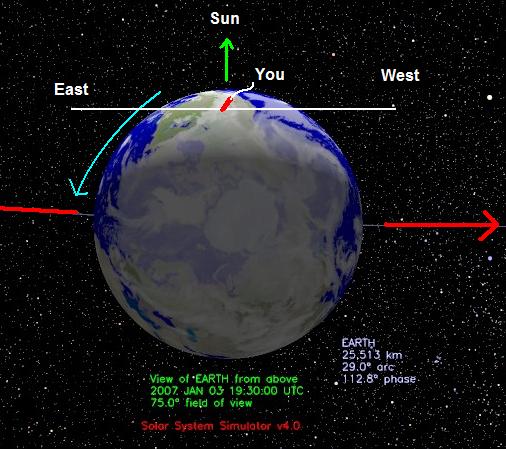
Figure 35 - View from above Earth at 1/3/2007 at 19:31 UTC. Image courtesy NASA/JPL-Caltech
|
At local apparent midnight using the compass points
You also can tell the direction that the Earth is moving at night using a watch to mark solar midnight - the mid-point between sunrise and sunset. Use the same procedure as described for solar noon and consult your online or local disk planetarium software for the constellation and nearest bright star that "souths" at that moment. At local solar midnight and facing south, the east on your left-hand and the west is on your right. At that moment, the Earth is moving towards your local due east and away from your local due west. See Figure 35 above.
Summary
The following table summarizes these key times when the direction that the Earth is moving in its orbital path at certain key times:
Table 2. Summary of key times and related direction of the Earth's orbit
| Key time | Moves toward | Moves away from |
|---|
| Sunrise | Toward from intersection of meridian and ecliptic between zenith and due south | Not visible - blocked by Earth |
| Local apparent solar noon | Towards due West | Away from due East |
| Sunset | Not visible - blocked by Earth | Away from intersection of meridian and ecliptic between zenith and due south |
| Local apparent midnight | Towards due East | Away from due West |
| First Quarter Moon | Not visible - blocked by Earth | Away nearly from the Moon |
| Full Moon | Towards due East | Away from due West |
| Third Quarter Moon | Towards nearly the Moon | Not visible - blocked by Earth |
References
Evans, James. 1998. The History and Practice of Ancient Astronomy. Oxford Univ. Press. ISBN: 0195095391
Minnaert, M. 1954. The Nature of Light and Colour in the Open Air. Dover. 1954nlco.book.....M
Schlosser, W., Schmidt-Kaler, T. Milone, E.F. 1991. The Vault of the Heavens. (Chap. 1). In Challenges of Astronomy. Springer-Verlag. 1991cahe.book.....S
Content-Child Safe Ratings

Copyright
No copyright is claimed as to any original materials on this web document. All original content by this author is released to the public domain. This website makes use of external content links that may be subject to copyright protection. No claim to copyright is made as to these linked external sources or any other external linked reference source.
Prepared by K. Fisher fisherka@csolutions.net Org. 12/28/2006 Rev. 12/29/2006
|


























